Min-Max Normalization

I was working with some LLMs, and I need to compare a set of LLMs based on metrics like Latency, GPU Power Usage, Alignment, Similarity, Clarity, and Conciseness for 9 Open Source LLMs. So I thought Spider/Radar Chart would be the best to show the comparison in a single graph. On plotting my data directly I got

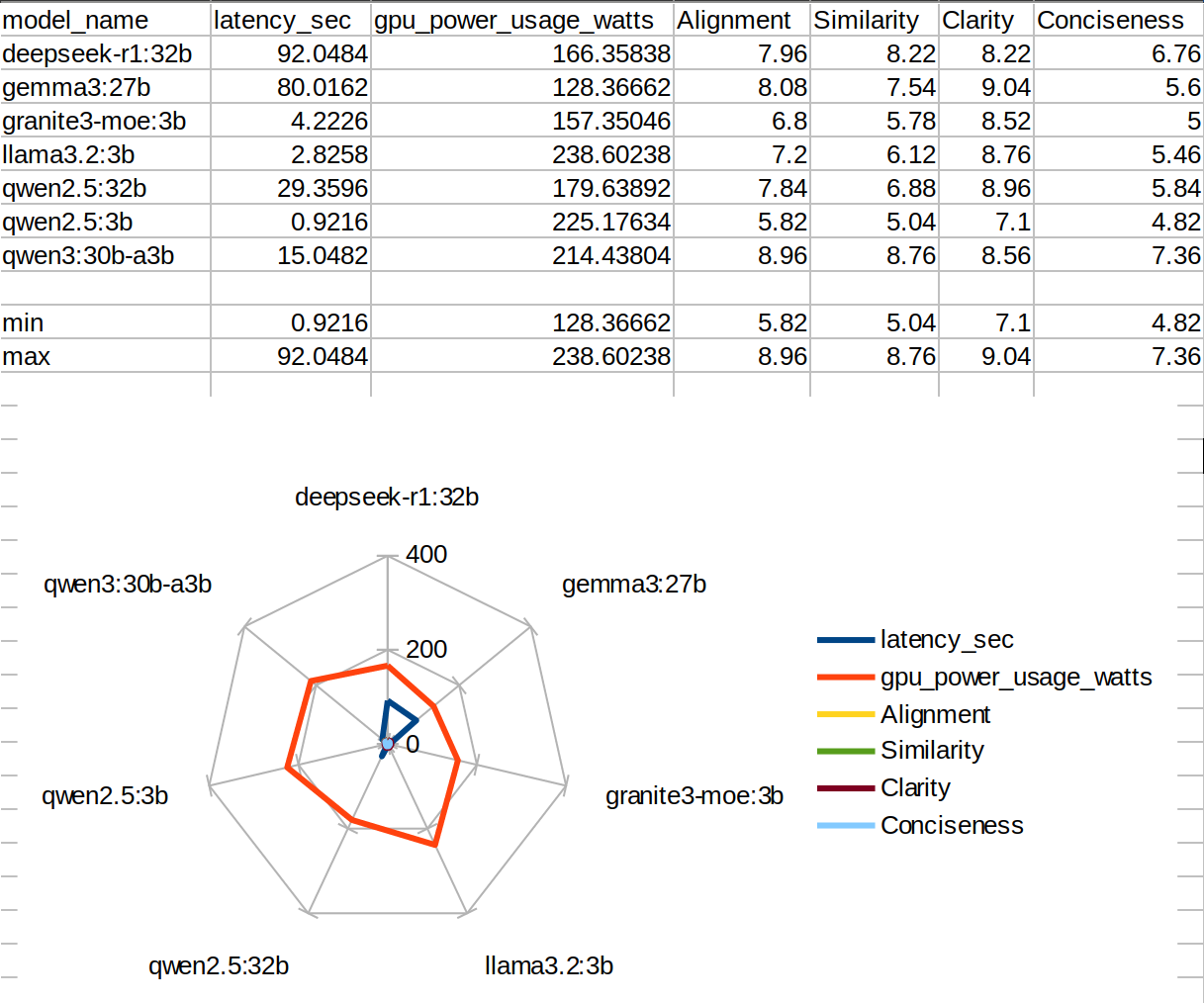Before Normalizing

See, the scaling of my data was wrong, as Alignment to Conciseness was scaled between 0-10 and the other two has no standard scaling. So I need to bring the Latency and GPU Power Usage values between 0 to 10. So the solution was Min-Max Normalization.

$$\begin{gather*} Min-Max\;Normalization=\left[\frac{(x−min(x))}{(max(x)−min(x))}\right] \times (new\_max - new\_min) + new\_min\\ \hspace{-5.3cm} min(x) \; \text{is the minimum value in the data range to be scaled} \\ \hspace{-5.2cm} max(x) \; \text{is the maximum value in the data range to be scaled} \\ \hspace{-6cm} new\_min(x) \; \text{is the min value of new scale (0 in [0, 10])} \\ \hspace{-5.7cm} new\_max(x) \; \text{is the max value of new scale (10 in [0, 10])} \\ \end{gather*}$$

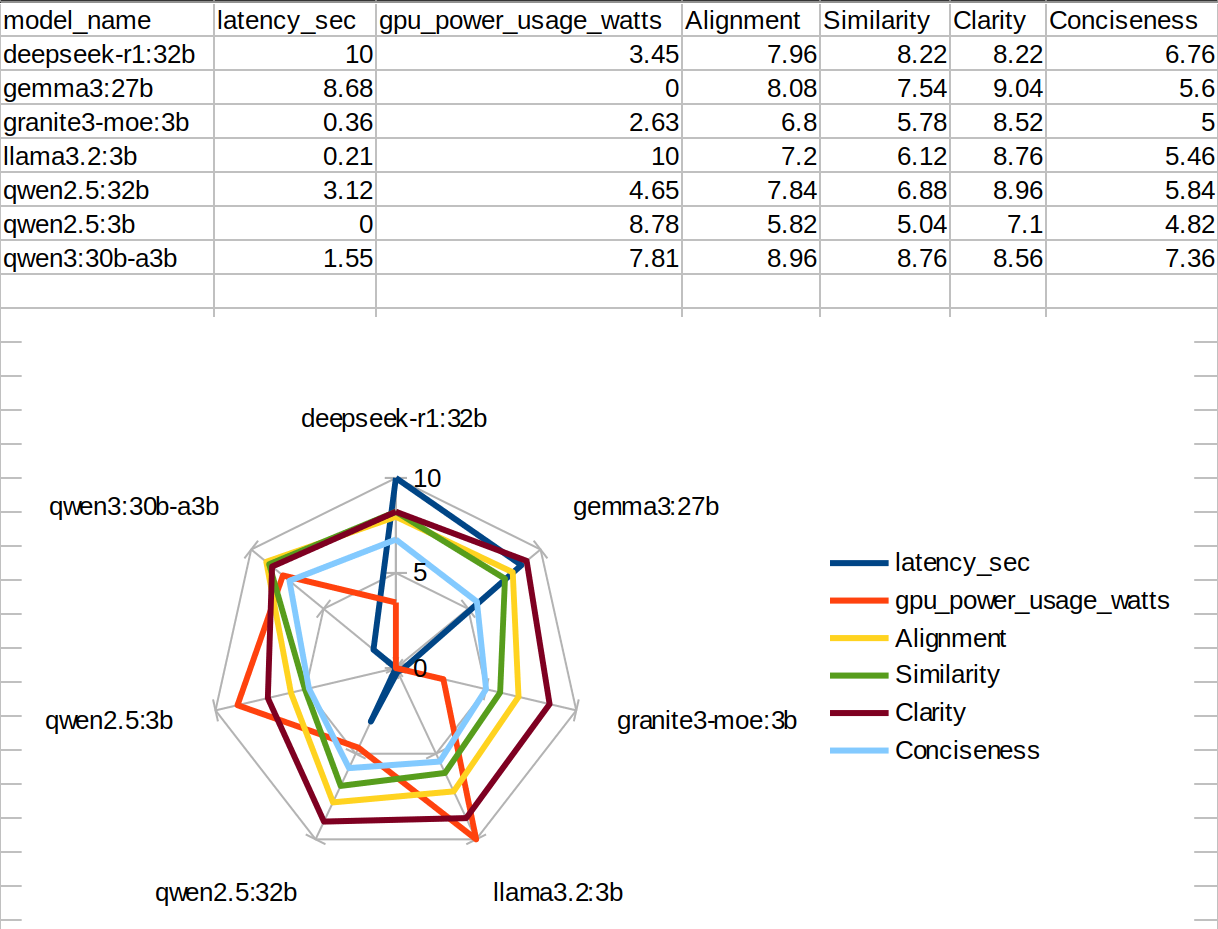After Normalizing

Note: Though it seems to be working(clearly plotting all values), just take a look at gemma3:27b's gpu_power_usage_watts and qwen2.5:3b's latency_sec - they're 0. This doesn't mean they didn't used gpu or fast answering, but a common error in min-max normalization. There are many solutions - Add a small constant (Additive to Smoothing) denominator and numerator, Log-Scale Transformation [$X\_log=log(X+1)$, the apply min-max norm to $X\_log$]

Now an Example:

We have values [23, 37, 11, 76] and the requirement is to scale it between 0-10, i.e, $min(x) = 11,\; max(x) = 76,\; new\_max = 10,\; new\_min = 0$

$$\begin{gather*} \text{Equation becomes:} \\ \\ \Longrightarrow \left[\frac{(x−11)}{(76−11)}\right] \times (10 - 0) + 0 \\ \\ \Longrightarrow \left[\frac{(x−11)}{(65)}\right] \times 10 \end{gather*}$$

Now we can put all the x(s) and get the min-max normalized values

Real Values	New Values
23	1.8
37	4
11	0
76	10

Python Code Snippet for Min-Max Normalization:

normalized = ((values - old_min) / (old_max - old_min)) * (new_max - new_min) + new_min

---

Normalization vs Standardization vs Scaling

Concept	Definition	Formula	Range	Use Case
Normalization	Rescales values to a fixed range (usually [0, 1] or [0, 10])	$\frac{x - \min(x)}{\max(x) - \min(x)}$	Any range	Visualizations, ML when scale matters (e.g., KNN)
Standardization	Centers data around mean 0 and standard deviation 1	$\frac{x - \mu}{\sigma}$	Mean = 0, SD = 1	When data is Gaussian, or algorithms assume zero-centered data
Scaling	Generic term – includes both normalization and standardization	N/A	N/A	Any transformation to bring values into a defined scale